Introduction
Unmanned Aerial Vehicles (UAVs) are used in a wide range of applications, from tracking and monitoring animals in remote areas to military applications. In general, drones are used to search, identify and monitor interesting events over massive and/or inaccessible areas. In order to effectively accomplish the task, multiple UAVs are deployed in a certain area and are expected to coordinate actions in an autonomous fashion or execute direct instructions from a control center.
In many scenarios, the UAVs need to exchange a relatively large amount of data among themselves and/or with the control station to support a given service. For example, distributed area monitoring/patrolling applications may require the UAVs to stream high definition video or thermal camera recordings to the control station, which demands wideband communication technologies (e.g., mmWave) that typically have limited coverage range. Therefore, providing such services over wide areas may require multi-hop data connections, where the UAVs themselves can act as relays for other nodes in the network.
On the other hand, UAVs and the control station also need to exchange light control traffic, which usually has strict latency and reliability constraints, but low transmission speed requirements. This traffic can be carried by low-rate long-range communication technologies, such as LoRa, so as to realize direct links between the UAVs and the control center. For example, this control channel can be used by the UAVs to send periodic tracking updates to the control center, which can use these messages to track the UAVs position. In these scenarios, UAVs and the control center can use different technologies to carry information and signaling traffic, physically separating the data and control planes. However, the randomness in the drones’ movements makes the design of a multihop routing protocol for the data plane a challenging problem.
In this article, we show the design for Stochastic Multipath UAV Routing for FANETs (SMURF) protocol, a centralized multipath routing protocol for FANETs, which exploits the tracking information available at the control center to estimate the reliability of routes and select the set of routes that guarantee the overall highest reliability. The routing tables can be computed by the control center and propagated to UAVs by using the Software Defined Networking (SDN) paradigm.
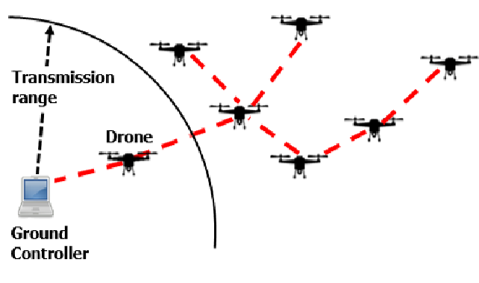
System Model and SMURF Protocol Definition
We model a FANET as a time-varying graph ![]() , where
, where ![]() is the set of UAVs in the network and
is the set of UAVs in the network and ![]() is the set of existing links at time
is the set of existing links at time ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We assume that the real position ![]()
![]()
![]()
![]()
![]()
![]()
![]()
(1) ![]()
![]()
where
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2) ![]()
![]()
If all links were independent as typically assumed in the literature, we would have
Once we have found the optimal route ![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3) ![]()
![]()
where
Link existence probability
We now assume that the estimated position distribution for each node is a multivariate Gaussian distribution, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(4) ![]()
![]()
Hence, the link existence probability as expressed in (1) is given by:
(5) 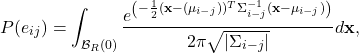
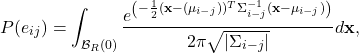
where ![]()
![]()
![]()
![]()
We now consider the existence probability ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(6) ![]()
![]()
where ![]()
![]()
(7) ![]()
![]()
All the computations above are so reduced to the calculation of multivariate Gaussian integrals, which can be performed efficiently with well-known numerical methods. Since the routing algorithm is executed by the control station, which should have sufficient computational power, there are no issues with the limited battery and computational capabilities of the UAVs.
Routing Metric Calculation
In order to compute the existence probability of a route, we need to consider all of its links jointly. In the following, we simplify the probability calculation by assuming that links that do not share nodes are independent, so that we can write:
(8) ![]()
![]()
This simplification is justified by the fact that each UAV’s movement is assumed to be independent, so that it is reasonable to expect that the mutual dependence of links that do not share nodes is negligible. By considering only the dependence on the immediately previous link, we can efficiently build a spanning tree by using the negative logarithm of the link existence probability as a routing metric:
(9) ![]()
![]()
In this way, links with a higher existence probability are chosen by the routing algorithm.
Backup Routes Calculation
By definition, the primary route is the one with the highest probability of existence, but it might still fail in a dynamic scenario. For this reason, we consider a set of backup routes, which can be selected in case the primary one fails. This can significantly increase the reliability of the transmission if the UAV swarm is dense enough, as there will be multiple viable routes to the destination. In order to calculate the optimal backup, we consider single-link failures and define the conditional path existence probability, given the link is down, as follows:
(10) ![]()
![]()
If the ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(11) 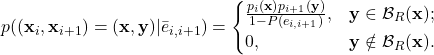
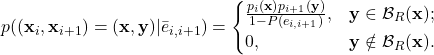
We can then adjust other links’ existence probabilities with such a conditional PDF and rebuild the spanning tree to find the backup route. After computing the optimal backup ![]()
![]()
(12) ![]()
![]()
where
Route information propagation and data plane
In our model, routing calculations are performed by the central control station, which collects tracking information using LoRaWAN and computes the routes. This centralized strategy provides two key benefits: first, the information collection and decision-making is in one place, so that the routing protocol inherently avoids loops and does not operate on contradictory information. Second, UAVs are spared from the computational load to perform numerical integration and calculate the route existence probability. The central node is not so constrained, and can even offload computation to the cloud.
The propagation of the routes to UAVs can be performed via SDN. This paradigm involves a central controller gathering information and sending simple instructions to switch nodes, and it has already been proposed and tested in FANETs. SDN also gives UAVs the possibility to send data over multiple interfaces, so the routing protocol could be implemented in an entirely transparent way, without requiring changes to the applications transmitting the data. Furthermore, SDN has been widely deployed in wired networks, and all major operating systems now support it by default.
The use of backup routes can increase the reliability of the transmission, but there is a trade-off: if packets are sent over multiple routes by multicast, this requires additional energy consumption and increases the load on the network.
Simulation and Results
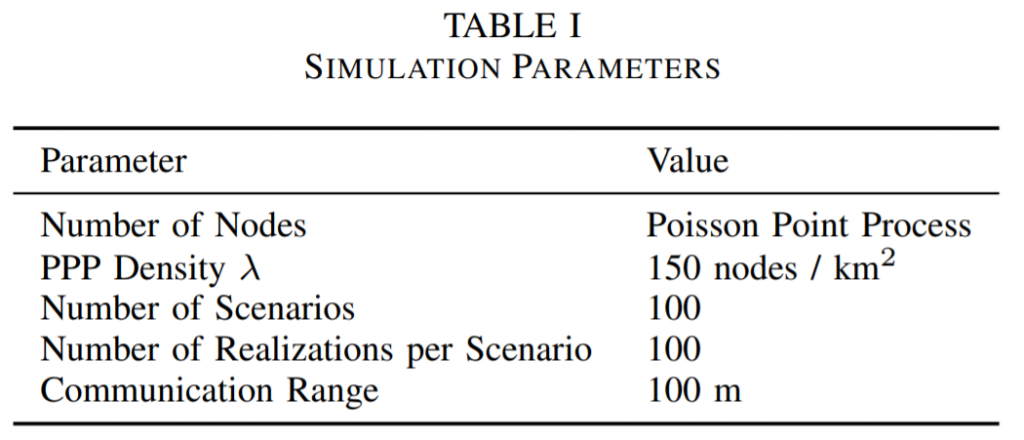
We design the simulation based on the parameters defined in Table I.

We compare our protocol with a single path algorithm based on a distance metric defined in. The protocol defined in the paper also contains a mobility metric. The velocity in the routing metric is considered to be the variance of the multivariate Gaussian distribution. Also, as mentioned before, the routing calculations are performed by the control center using the Kalman tracking algorithm fed by the position updates through LoRaWAN. We ran a shortest path algorithm, as mentioned in, to get the path from source to destination. We also considered the theoretical oracle routing protocol, which operates with perfect information about the UAVs’ positions and, consequently, the existence of the routes.
The performance measure considered to evaluate the routing protocol is the Packet Delivery Ratio (PDR), as the goal of the work was to increase reliability. To calculate the PDR in MATLAB, we consider the existence of paths between all the nodes in primary and/or backup routes. If at least one of the selected routes exists for a particular realization of the distribution, we consider the packet to be delivered correctly, while when none of the selected paths exists, the packet delivery fails. Additionally, the packets are multicasted over the primary and backup routes so as to avoid additional energy consumption due to duplication of packets on links shared by such routes. Finally, we have assumed that there is no radio interference between the packets sent on multiple routes. We evaluate the delivery for every realization in every scenario and plot it as a boxplot. Fig. 2 shows the packet delivery ratio when incorporating multiple routes from source to destination, with a density ![]()
![]()
![]()
![]()
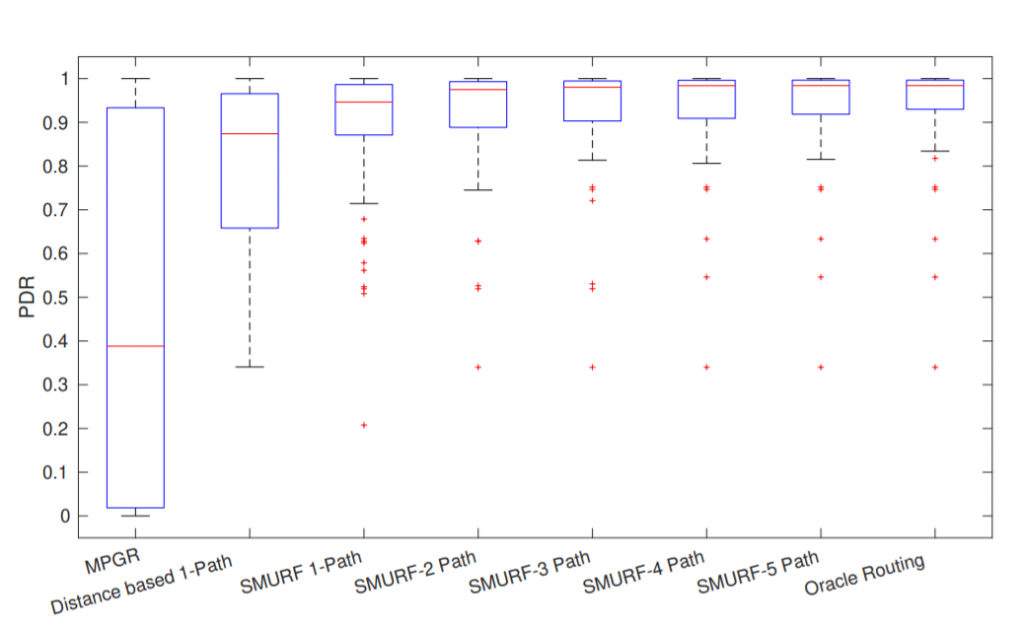

The boxplot shows the empirical distribution of the PDR for the given scenario. The average PDR for SMURF is significantly higher even when considering a single path: while the distance-based protocol has an average PDR of 85\% and an existing mobility based geographic routing protocol, MPGR [14] is below 40\%, SMURF can achieve 93\%. MPGR performs even worse than the distance-based metric, as shown in the figure. Furthermore, the lower quartile edge of the boxplot shows that the distance-based protocol performs far worse in the worst cases, with 25\% of possible network graphs having a PDR of 70\% or lower, while single-path SMURF achieves an 88\% PDR for the 25th percentile graph. This gain comes from the fact that SMURF computes the route existence probability accounting for the inter-dependency of adjacent links. The gains become even more significant when considering multiple routes: using 2 paths improves the average PDR to about 98\%, and 3-path SMURF already has a performance very similar to the oracle routing protocol i.e. maximum achievable routing performance when all positions are accurately known by the control center. This justifies the need for backup routes, but also limits the algorithm to a small number of alternative paths, which helps reduce the overhead due to packet replication.
Conclusion
In this work, we propose a statistical analysis of a FANET with tracking information and derive the existence probability for both single links and entire routes. We then design SMURF, a multipath routing protocol that computes a primary route (i.e., the route with the highest existence probability), and a series of backups that allow the transmission to succeed even if a link in the primary route is broken. Even with just two backup routes, the protocol’s performance is very close to the optimum, represented by the flooding strategy, with a far lower waste of bandwidth.
For more details, check out the full paper at SMURF: Reliable Multipath Routing in Flying Ad-Hoc Networks | IEEE Conference Publication | IEEE Xplore.