Optimizing On-demand Slices Selection in Core Networks

The evolution of wireless core networks provides a ﬂexible framework for network traﬃc management. The most famous concept is network slicing.

In this article an on-demand network slices selection problem in the core network will be introduced in section 1, and the optimization formulation of the slices selection problem will be deﬁned in section 2. In section 3 I will demonstrate my implementation of the purposed solution by simulation and also the simulation results. Lastly, a conclusion will be presented in section 4.

1 Introduction

According to 3GPP standardization, the simplest telecommunication net-work consists of a core network, a radio access network and User Equipment (UE). For instance, a 5G network contains a 5G Access Network (5G AN) and a 5G Core Network (5GC) [3]. A 5G AN is an access network comprising a Next Generation Radio Access Network (NG-RAN) and/or a non-3GPP Access Network (AN) connecting to a 5GC. An NG-RAN consists of base stations, which are called Next Generation NodeB (gNodeB, or gNB) and Next-Generation E-UTRAN NodeB (ng-eNB). From a system level point of view, the above architecture was enhanced by Network Function Virtual-ization (NFV), Software-Deﬁned Networking (SDN) [2] [1]. In particular, Network Slicing original from SDN and NFV provides ﬂexible end-to-end support for network traﬃc management.

Moreover, the 3GPP architecture also provides diﬀerent Network Func-tions (NF) [5] [4] to control and operate the network. Speciﬁcally, Network Slice Selection Function (NSSF) helps the UE in the network with ﬁnding the proper network slice (virtualized network function) instance. The slice selection procedure will consider the QoS or service-level agreement that the UE engaged. However, the further implementation or proof of concept related to the NSSF is still open for customization. This article presents an abstract model for decision at NSSF to allow the optimizing selection of network slices.

2 Problem Formulation and Optimization Method

To formulate the problem, we consider the following model:

Let $S \in \mathcal{N}^{m}$ be the set of all available slices and $R(t) \in \mathcal{N}^{n}$ be the set of all flow requests from all UEs at time $t$ .
The slice selection can be modeled as the edges set, $E$ , which is connected between $R(t)$ and $S$ .
Therefore, we have a graph $G = (R(t), S, E)$ such that each request node $r \in R(t)$ has only one edge $e_{r,s} \in E$ ( $E \in \mathcal{N}^{m*n}$ )to a slice node $s \in S$ at time $t$ .
The set $E$ in graph $G$ presents a possible selection at time $t$ .

(1) $\begin{equation*}e_{r,s} = \begin{cases}1, \textrm{if a selection between } r,s \textrm{ is established}\\0, \textrm{otherwise}\end{cases}\end{equation*}$

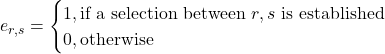
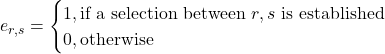
Moreover, we consider the weight of each edge between any $r$ and $s$ nodes is $w_{r,s}$ .
The edge weight can represent the cost to transmit the UE traffic over the selected slice.
The above model can be mapped to an integer programming problem as below.
Thus, the optimization goal is transferred to minimize the total cost in the network and the objective function is:

(2) $\begin{equation*}\begin{array}{l}\min \sum\limits_{r \in R(t), s \in S} w_{r,s}e_{r,s} \\ s.t.\\\sum\limits_{r \in R(t)}e_{r,s} \leq 1, \forall s \in S \\\sum\limits_{s \in S}e_{r,s} \leq 1, \forall r \in R(t) \\e_{r,s} \in \{0,1\}, \forall r \in R(t), \forall s \in S\end{array}\end{equation*}$

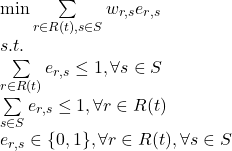
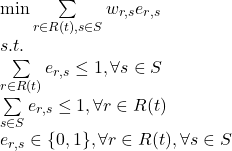
Because the integer programming problem had been proved to be NP-hard [6], we need to apply some relaxation to solve it. Therefore, we use Lagrangian relaxation method [8] and a branch and bound solver [7] to solve the relaxed problem.

The relaxed problem can be rewritten as below:

(3) $\begin{equation*}\begin{array}{l}\min \sum\limits_{r \in R(t), s \in S} w_{r,s}e_{r,s} - \sum\limits_{r \in R(t)} \lambda_{r} (\sum\limits_{s \in S} e_{r,s} -1)\\ s.t.\\\sum\limits_{r \in R(t)}e_{r,s} \leq 1, \forall s \in S \\e_{r,s} \in \{0,1\}, \forall r \in R(t), \forall s \in S\end{array}\end{equation*}$

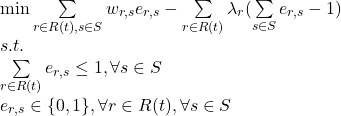
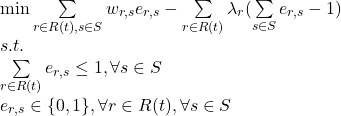
3 Simulation

We assume the network system executes in a time-slotted environment. Hence, a discrete-time event simulator is used to simulate the network traffic demand from UEs. At each time slot $t$ , some flows are generated and every flow shall be transmitted over a network slice.
The network traffic demand is determined by a traffic generation rate, $\alpha$ which is a random variable.
If $\alpha_{r} > 0$ at slot $t$ , a traffic flow $r$ will be generated at slot $t$ .
When a traffic $r$ was generated, the traffic volume, $v_{r}$ , and the expired time, $l_{r}$ , were also defined based on the UE’s QoS requirements.
On the other hand, the available network slices’ status will be updated at every time slot.
Each slice has a predefined data rate, $b_{s}$ . Therefore, the cost to transmit a flow over a slice can be defined as below:

(4) $\begin{equation*}w_{r,s}=\begin{cases}$b_{s} / v_{r}$, \textrm{if} $b_{s} \geq v_{r}$ \\$v_{r} / b_{s}$, \textrm{otherwise}\end{cases}\end{equation*}$

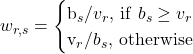
If the traffic flow $r$ can be transmitted with proper slice $s$ , then the traffic flow $r$ will be transmitted at slot $t$ . Otherwise, the traffic flow $r$ will be put in a waiting queue and wait for the next available time slot. The transmission time delay will be the summation of the queue waiting time and the transmission time of each flow.
If the transmission time delay is larger than the expired time, $l_{r}$ , the flow will be counted as a fail transmission.

Moreover, a greedy algorithm is used as a benchmark to compare with the branch and bound algorithm.
At each time slot $t$ , if there is an available slice, the greedy algorithm will check every flow in the waiting queue and allocate the slice to a flow with minimal cost. The cost was considered as the transmission latency and the service-level agreement violation rate.

From Figure 1, the SOCP, a branch and bound algorithm, outperforms the greedy algorithm.

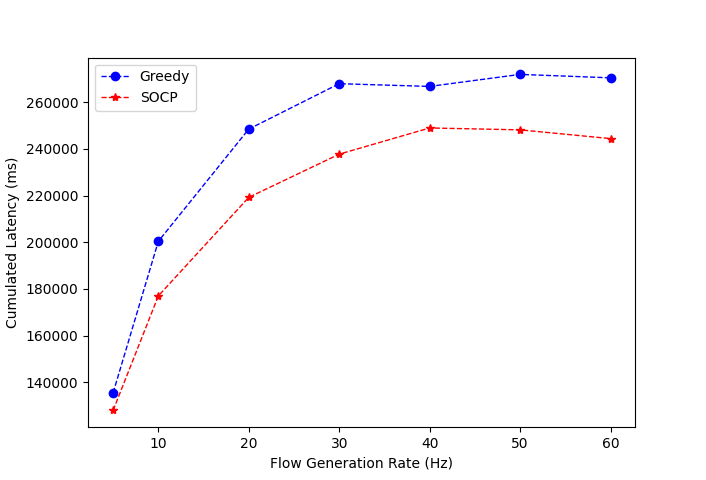
Figure 1

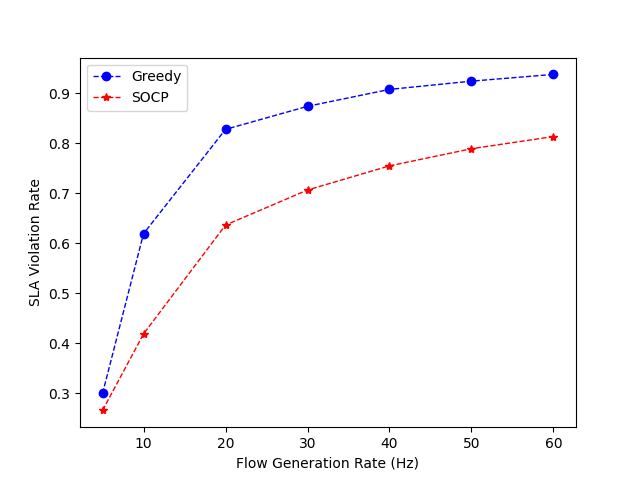
Figure 2

From Figure 2, the SOCP algorithm also has a better SLA than the greedy algorithm.

4 Conclusion

We introduce the network slices selection problem as an integer programming problem and then applying relaxation techniques to transform the problem into a solvable linear programming problem. In addition, from the simulation we compare the performance between the greedy algorithm and the branch-and-bound algorithm.

References

[1] 3GPP. Feasibility study on new services and markets technology enablers for enhanced mobile broadband; Stage 1. Technical Report (TR) 22.863, 3rd Generation Partnership Project (3GPP), 04 2016. Version 14.2.2.

[2] 3GPP. Study on Architecture for Next Generation System. Technical Report (TR) 23.799, 3rd Generation Partnership Project (3GPP), 04 2016. Version 14.2.2.

[3] 3GPP. System Architecture for the 5G System. Technical Specification (TS) 23.501, 3rd Generation Partnership Project (3GPP), 04 2018. Version 14.2.2.

[4] 3GPP. Telecommunication management; Study on management and orchestration of network slicing for next generation. Technical Report (TR)

28.801, 3rd Generation Partnership Project (3GPP), 04 2018. Version 15.1.0.

[5] 3GPP. 5G System; Unied Data Management. Technical Specification (TS) 29.503, 3rd Generation Partnership Project (3GPP), 04 2019. Version 16.

[6] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Cliord Stein. Introduction to Algorithms, Third Edition. The MIT Press, 3rd edition, 2009.

[7] Er Domahidi, Eric Chu, and Stephen Boyd. Ecos: An socp solver for embedded systems. In in European Control Convergence, 2013.

[8] Marshall L. Fisher. The lagrangian relaxation method for solving integer programming problems. Management Science, 50(12 supplement):1861 {1871, 2004.

August 6, 2021

Research

5G, Optimization, Wireless Communication