Curriculum Learning for mmWave Beam Selection

Curriculum Learning

Curriculum Learning [1] is a biologically inspired procedure to train machine learning models. While it is usual practice to train Neural Networks (NNs) using batches of data sampled uniformly in random from the training dataset, curriculum learning mimics the way humans learn, starting from simpler training samples that unveil general and raw concepts, and then moving to harder ones that provide finer details about the concept to be learnt. To apply this strategy it is necessary to first define scoring and pacing functions: the former assigns a level of difficulty to each sample, while the latter determines at which rate the transition should be made from easier samples to harder ones during the learning process. The survey paper [2] provides an extensive treatment o curriculum learning and its application in various branches of machine learning. In the following, we will introduce a fundamental problem in 5G networking — the mmWave beam selection — and showcase the benefits of curriculum learning in this context.

mmWave Beam Selection

Millimeter wave (mmWave) communication constitutes a fundamental technology in 5G and future networks, which allows overcoming communication bottlenecks of the over-exploited sub-6GHz bands. To overcome the severe propagation impairments of the above-10GHz spectrum, such as high path attenuation and penetration losses, mmWave communication systems employ a massive number of antennas at the base station (BS) to form highly directional beams and attain a large beamforming gain. Due to the narrow mmWave beamwidth, extremely precise alignment and tracking procedures are necessary in order to establish a reliable and high throughput communication link. The beam selection problem boils down to determining which is the best directional beam at the transmitter side and at the receiver side in order to establish a reliable communication link. The optimal communication beam can be easily determined with full channel knowledge; however, in the large antenna regime, obtaining an estimate of the high dimensional channel matrix is costly; hence, beam selection requires lengthy iterative search procedures that sequentially test different beam directions. Alternatively, it has been recently shown that contextual information from sensors mounted on the user equipment and the infrastructure can be leveraged to reduce the beam selection overhead. This is practically done by formulating the beam selection problem as machine learning classification task to predict the best beam direction from sensory data. An important peculiarity of the beam selection problem is that in the absence of line-of-sight (LOS) the predictability of the strongest propagation paths greatly decreases as a consequence of the prominent dependency on the relative positions of scatterers and reflectors. The difficulty of the prediction task in NLOS scenarios is so high compared to the LOS case that data-driven methods tend to be biased towards the easier LOS samples to the detriment of the NLOS performance. For this reason, the absence of LOS is a natural notion of difficulty that can be exploited to define a curriculum learning strategy to train beam selection ML models.

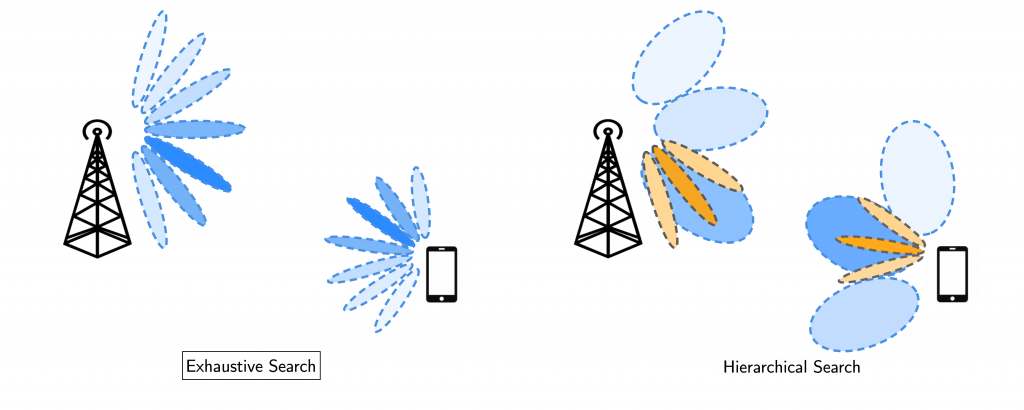
*Fig.1* Two examples of Beam Selection algorithms, the coordinated Exhaustive Search in which both ends sequentially sweep through the beam codebooks, and the Hierarchical Search in which the search is performed starting from wide beams and then refined using finer ones.

Sensor-based Beam Prediction with Curriculum Learning

In this section we focus on the ML problem associated with the sensor-aided beam selection problem. Namely, the task of learning the relationship between the sensor information and channel measurements. Given the natural notion of hardness in the previous section, we now define an effective way to modulate the difficulty of this learning task. A straightforward approach consists of changing the probability of NLOS samples during the training epochs. Hence, denoting by $P$ the feature distribution from which the original training dataset $\mathcal{D}$ is generated, we exploit a biased sampling scheme to generate a skewed dataset $\mathcal{D}(\lambda)$ , whose hardness is proportional to the rejection coefficient $\lambda\in [0,1]$ . In particular, the set of instances $\mathcal{D}(\lambda)$ is created from $\mathcal{D}$ by independently removing each NLOS sample with probability $1-\lambda$ . As a result, $\mathcal{D}(\lambda)$ represents a sample drawn from the following distribution

(1) $\begin{align*}P(\lambda)\propto(1-q)P_{LOS}+q\lambda P_{NLOS}\end{align*}$

where $P_{LOS}$

is the feature distribution conditioned on the presence of LOS, $P_{NLOS}$

is the distribution conditioned on its absence, and $q$

is the probability of NLOS condition under the original distribution $P$

.
The pacing function is represented by a sequence ${\lambda_i}$

that for each epoch $i$

determines the probability that a NLOS sample is accepted for training. A properly chosen sequence ${\lambda_i}$

can improve both the convergence speed and the accuracy of the final solution compared to the unstructured and randomized sampling of training instances.

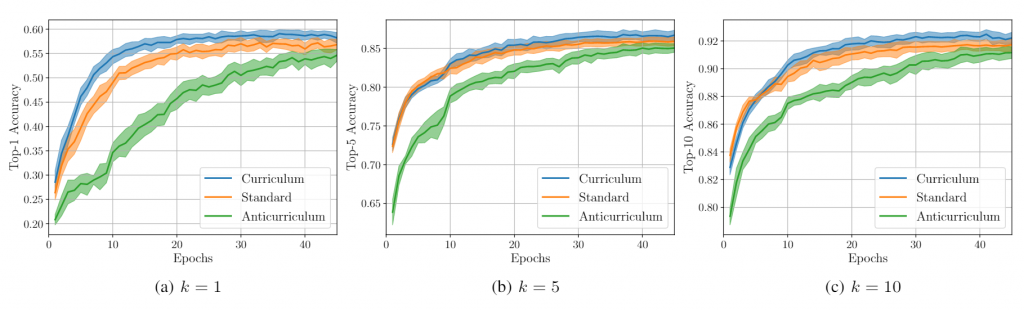
In the Fig.2 we illustrate the benefits of biasing the sampling procedure in order to obtain a sequence of training samples with an increasing level of difficulty. We employ the sample rejection strategy based on the described above. Specifically, we train the proposed NN architecture for 45 epochs, decreasing the NLOS rejection probability $1-\lambda$ from 1 by steps of 0.2 every 9 epochs until reaches 0. In this manner, the first batches contain only LOS samples, whereas during the last 9 epochs the ratio between LOS and NLOS will be the same as the one in the original unbiased empirical distribution. We also consider the opposite strategy, namely exposing the NN to batches of hard samples first. This is obtained by the same sampling procedure but with the role of NLOS and LOS swapped. We term this alternative anti-curriculum as it starts from the hardest instances. As a natural baseline, we also consider the standard unbiased sampling procedure. For each case, we train the same model architecture using the loss function with $\beta=0.8$ . Distinct training dynamics result in different convergence time and final accuracy values. We plot the evolution of the accuracy metrics, averaged over 10 repetitions, of the standard, curriculum and anti-curriculum learning procedures. In terms of convergence time the curriculum learning strategy outperforms both the standard and anti-curriculum sampling schemes as it quickly plateaus to higher accuracy levels. The curriculum learning strategy improves by $2\%$ the top-1 throughput ratio and by $1.2\%$ the top-5 throughput ratio compared to standard learning. On the other hand, anti-curriculum learning has a detrimental effect on the performance, resulting in a performance loss of $4\%$ and $1.7\%$ in terms of top-1 and top-5 throughput ratio, respectively.

*Fig.2* Evolution of the top-k accuracy over the training epochs for curriculum, standard and anti-curriculum training approaches. The curves are averaged over 10 training runs.

References

[1] Bengio, Yoshua, et al. “Curriculum learning.” Proceedings of the 26th annual international conference on machine learning. 2009.

[2] Soviany, Petru, et al. “Curriculum learning: A survey.” arXiv preprint arXiv:2101.10382 (2021).

[3] Zecchin, Matteo, et al. “A Novel Look at LIDAR-aided Data-driven mmWave Beam Selection.” arXiv preprint arXiv:2104.14579 (2021).

November 28, 2021

Research

Machine Learning, mmWave Beam Selection, msca, phd, researcher

Curriculum Learning for mmWave Beam Selection

Matteo Zecchin