Millimeter Wave (mmWave) communication, offering wide bands, is a key enabling technology of Fifth Generation (5G) and Beyond 5G (B5G) communication systems to handle the explosive demand for high data rates. Beamforming and Massive Multiple-Input-MultipleOutput (mMIMO) antenna arrays at the Base Stations (BSs) are expected to provide directionality and beamforming gain to combat the high propagation loss that characterizes
mmWave communications. Therefore, precise beams alignment is necessary for maintaining the quality of service.
In 5GNR, the large number of beams makes conventional beam sweeping approaches for beam management challenging. Exploiting location-side information has been shown to be beneficial in speeding up beam training. However, acquiring and transferring location information is by itself an additional overhead to the communication system and energy-consuming. We devise a beam selection method in mmWave systems based on the relative location of User equipments (UEs) in a cell provided by Channel Charting (CC). The beam selection problem has been addressed in two ways: First, we focus on beam handover in one BS by predicting the SNR of other beams based on CC. Second, in a non-standalone system, mmWave beam is predicted based on Sub-6 GHz BS CC
CHANNEL CHARTING
Channel charting [1] is a self-supervised framework for pseudo-localization and tracking of UEs using dimensionality reduction in the channel state information (CSI) domain. This technique learns a charting function over a specific channel, which maps high-dimensional CSI to low-dimensional pseudo-locations. Moreover, the function is learned in a self-supervised manner, without any need for ground truth location information. Successful channel charting relies on two aspects: (i) carefully designed CSI features, as CSI measurements are prone to a variety of system and hardware impairments, such as noise, small-scale fading; and (ii) the dimensionality reduction method.
In channel charting, CSI features are first extracted for each UE. Then, the set of features is transformed to a lower dimension using Dimensionality Reduction (DR), typically based on pairwise feature distances between the UEs. Here, we used covariance matrices as UE features. To measure the feature dissimilarity, we use the Log-Euclidean distance between the covariance features of UEs. The dissimilarity matrix is fed to a DR algorithm to obtain a 2D representation of the CSI of the set of UEs, the CC. For DR, we shall use ISOMAP, and t-Distributed Stochastic Neighbor Embedding (t-SNE). The obtained charts are expected to preserve neighborhood relations of the physical locations of the UEs.
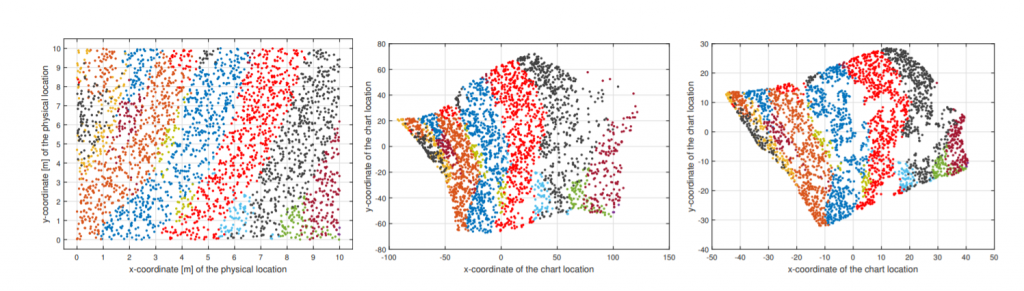
colors. For example, beam 32 is the best beam for the locations marked with red. CC
annotated with best beam information using: (Middle); ISOMAP DR. (Left); t-SNE DR
As an example in Figure 1, we consider the 10×10 m street segment with 3000 ground truth sample locations of the UEs, and a color-coding according to the best mmWave beam. The CC is constructed from the dissimilarity matrix using the ISOMAP and t-SNE DR techniques. The CCs show a good approximation of the physical locations of the UEs with the general global structure and spatial distribution pattern maintained by the t-SNE CC in
particular.
BEAM PREDICTION
We consider Beam-CC-based Network Centric Handover. The basic principle is that each beam has a CC constructed offline and the CC locations are annotated with SNRs of neighboring beams. A prediction algorithm then predicts the SNR of a target beam. The annotated CC and the SNR prediction algorithm are then used to make a beam handover decision. The Network Centric model is illustrated in Figure 2. The Training phase consists of creating
channel charts, annotating with neighbor beam SNRs, and training of the SNR predictors. In the online phase, the current beam CC location and SNR are used to predict the SNR at a target beam. In the non-standalone system similarly, the same approach is adopted. The differences are firstly a classification problem is solved, secondly, instead of having beam CCs, for the sub-6 GHz BS, one CC can be constructed and information of the mmWave system best beam can be added to the CC in an offline training phase. All information is gathered at a central control unit. Thus in the offline phase, the CC locations are annotated with best mmWave BS beam IDs. A prediction algorithm then predicts the best beam ID of the mmWave system for the CC location of a new UE.
In the online phase, for UE i which has established connection, the obtained SNR mapping function/beam ID predictor will be used to predict a target beam SNR / best beam ID.
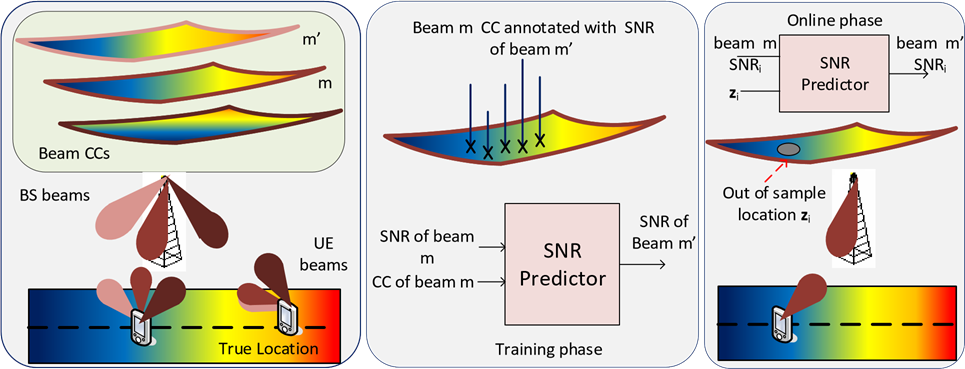
An out-of-sample extension of CC is performed to locate the new UE i on the CC with coordinates z. Then, the SNR of target beams / best beam ID is predicted based on the CC location of the new UE.
Given the annotated CCs, SNR / beam ID prediction can be formulated as regression/ classification problems. Supervised ML techniques assist us to find this function. The input to the predictor is CC location and outputs are either SNR of target beams or best beam ID. K-nearest Neighbors (KNN), Gaussian Process Regression (GPR), Support Vector Machine (SVM), and Neural Networks (NN) are considered for prediction.
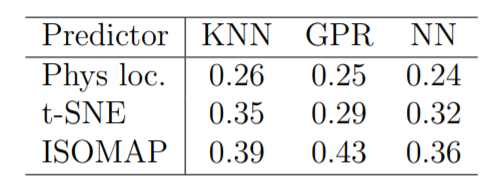
In the beam SNR prediction problem [2], we implement prediction based on CC and the true 2D physical location assuming that the physical location is known at the BS. For true location-based prediction, NN can achieve slightly better performance than KNN and GPR, at the cost of significantly higher computational cost in the training phase. In the simulated scenario, an error floor of 0.25 dB RMSE is found for prediction based on ground truth physical location. GPR using t-SNE CC is the best of the CC methods, exhibiting a 0.05 dB gap to the ground truth location-based prediction. Comparison results can be found in Table 1 where ”Phys Loc.” corresponds to the true 2D physical location.
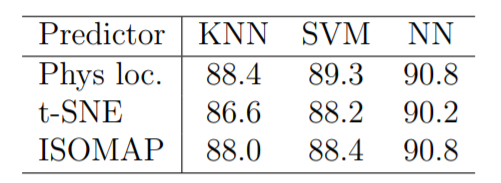
For the non-standalone system [3], the average prediction accuracies for CC-based and benchmark predictors using KNN, SVM, and NNs are compared in Table 2. NN outperforms SVM, which again outperforms KNN. The accuracy of the best predictor (i.e., NN) based on ISOMAP CC achieves the accuracy of prediction based on true location. The prediction accuracy of top-2 and top-3 best mmWave beams for best NN-based predictors is above 98 %. The top-2 or top-3 information can be used to reduce the best beam search time if this information is shared with the UEs. Accordingly, instead of searching over 32 beams, the search is carried over 2-3 beams.
To sum up, we have considered mmWAve system beam prediction based on CC. The beam prediction based on CC using NN matches the performance of a predictor based on true location, with high accuracy. The presented results show that CC can be used as a replacement for true location-based radio resource management.
References
[1] C. Studer, S. Medjkouh, E. G ̈on ̈ultas ̧, T. Goldstein, and O. Tirkkonen, “Channel charting: Locating users within the radio environment using channel state information,” IEEE Access, vol. 6, pp. 47682–47698, 2018.
[2] P. Kazemi, T. Ponnada, H. Al-Tous, Y. -C. Liang and O. Tirkkonen, “Channel Charting Based Beam SNR Prediction,” 2021 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), pp. 72-77, 2021.
[3] T. Ponnada, P. Kazemi, H. Al-Tous, Y. -C. Liang and O. Tirkkonen, “Best Beam Prediction in Non-Standalone mm Wave Systems,” 2021 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), pp. 532-537, 2021.